The Riemann zeta function is defined by the Dirichlet series
(1) 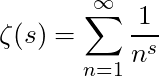
where it converges absolutely for ![]() . By the application of the Euler-Maclaurin formula
. By the application of the Euler-Maclaurin formula
(2) 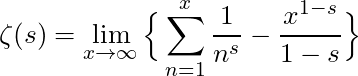
extends the domain of converge for ![]() . And by subtracting one more term
. And by subtracting one more term
(3) 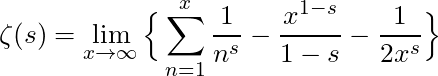
extends the domain of converge for ![]()
Integral Representation
(4) 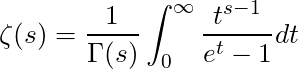
where it converges absolutely for ![]() .
.